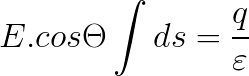When it comes to electric charge and field we almost know everything about it but what about Gauss law ? Gauss law is an important topic in this chapter but before going into Gauss law we need to understand what is Gaussian surface and how to determine a Gaussian surface?
Before proceeding about how to determine a Gaussian surface let’s first understand about what is a Gaussain surface.
Table of Contents
What is a Gaussian surface ?
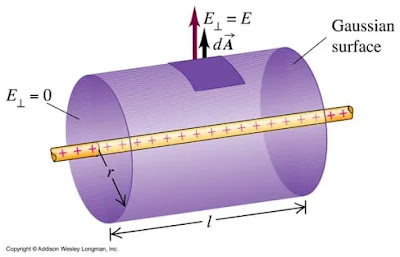
Surface on which angle (ө) between electric field (E) and area vector (A) is always constant at each and every point this kind of surface is know as Gaussian surface.
Maybe you didn’t understand the term electric field or area vector. So to know about electric field I have an dedicated article on electric charge and field so do read as well.
We know that vector quantity has magnitude and direction, therefore area vectors are vector of plane surface who’s magnitude is the area of surface and direction is perpendicular to the surface.
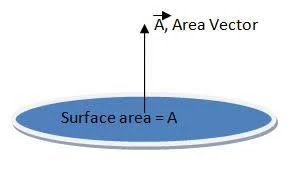 |
| Area vector |
Well how will you identify a Gaussian surface if you see one?
How to determine a Gaussian surface ?
We know that Gaussian surface follows Gauss law and angle (ө) between electric field (E) and area vector (A) is always same at each point. So to determine a Gaussian surface we just need to check if at each point on a surface angle (ө) is same or not.
Gauss law:
Here are the steps to determine a Gaussian surface:
Step 1: Select the surface from a body or object
So often people gets confused and they start to check whether angle is same for all point on a body or not. Well what you need to be clear is we want to identify whether a surface on a body is Gaussian surface or not and therefore check angle (ө) at every point on the surface and not on each and every point of whole body.
 |
| Identifying a surface |
In the above image we are considering non-shaded region to find whether it’s a Gaussian surface or not and shaded region is not considered because we need to find whether a surface in an object is Gaussian surface or not.
P.s: It means a body can have more than 1 Gaussian surface.
Step 2: Check direction of electric field (E)
Now after deciding the surface you need to check the direction of electric field from the surface.
From where electric field lines are going out on a surface.
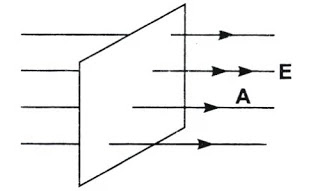 |
| Direction of electric field |
If you don’t know about electric field or electric field lines we have another article on this do read that as well because we have provided handwritten notes as well with each derivation of electric field and Gaussian surface and law as well. Click here to read that articke
Step 3: Check the area vector (A)
After checking the electric field direction you need to check the area vector of the surface. Area vector is actually vector who’s direction is always perpendicular to the surface.
Step 4: Check the angle between area vector (A) and electric field (E)
So after determining the direction of electric field and area vector now it’s time to find out the angle (ө) between them.
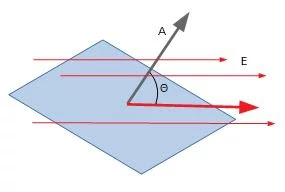 |
| Angle between area vector and electric field |
Check if angle between both of them is same at all the point. If Yes! then it’s a Gaussian surface.
Well, one question which may have strike you is why is it necessary to determine a Gaussian surface why is it so important?
Why is it necessary to determine a Gaussian surface and how does it help us ?
Gaussian surface helps us in evaluating electric field due to different charge distribution.
If you want to find about the evaluating electric field due to different charge distribution I have my personal notes uploaded on this site. Click here to go to article to download notes.
Some examples of Gaussian surface:
So some of the examples of Gaussian surface are:
1. Imaginary cylindrical Gaussian surface created to find out electric field due to a straight charged conductor. You will find this derivation in our notes as well 🙂
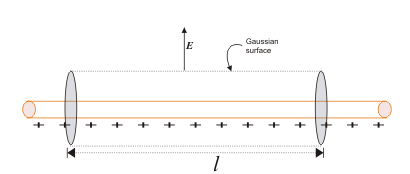
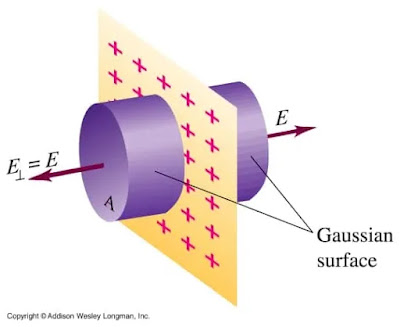
2. Imaginary cylindrical Gaussian surface created to find out electric field due to a plane charged sheet. You will find this derivation in our notes as well 🙂
 |