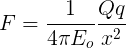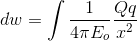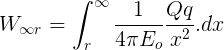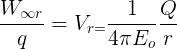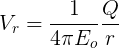Electric Potential at the Centre of a Ring - Derivation and Explanation

We know about the definition of electric potential but that’s not it, there are many more things in this particular field. Well, not just that but there are many more derivations linked to this like ‘electric potential at the centre of a ring’ (sounds little tough but I’ll make it easy for you guys to understand).

Electric potential at the centre of the ring is the same as the potential due to a point charge. Whereas the electric field is 0 at the centre of the ring because the electric field at the half side of the ring cancels out the other half.

Before understanding electric potential at the centre of a ring, you need to understand electric potential and electric potential due to a point charge.

Table of Contents

Proof of electric potential at the centre of the ring is the same as point charge:

Before Proceeding to prove that electric potential at the centre of the ring is the same as the electric potential due to a point charge we need to give a proper definition of electric potential first.

What is electric potential ?

So before understanding electric potential, let’s understand the meaning of potential. Potential is characteristic of a “Location” and potential energy is the characteristic of a charged particle.

Electric potential is the work done by an applied force on a unit charge bringing it from infinity to a specific point. The work done is called electric Potential.

Electric potential to infinity is zero.

Potential of a point:

Electric potential at point A

Potential

So, here in the above image VA represents the electrical potential at point A, this point A can be anywhere.

Now in order to calculate this potential for point A, we assumed that electric charge has been brought from infinity ‘ ∞’ to point A, now we don’t know how much far infinity is so we simply suppose the potential at infinity 0.

This difference between potential of point A and infinity is called the work done (W) in bringing the charge from infinity to the point.

So this is electric potential, where W is the work done on bringing a point charge from infinity ‘ ∞’ to point A and V is the potential at a point.

Suppose we bring a charge from infinity to a point so we need some force to do that work in bringing a charge from infinity to a particular place and this energy or work which is done is what we call as potential of a place.

P.s: The term potential is a location-based characteristic. Every place has different potential. Just like one end of a battery has high potential and another end has low so that’s why when we connect both the sides of a battery with wire, current flows in the direction of higher potential.

Now let’s define electric potential due to point charge:

Electric potential due to a point charge:

To find electric potential at a location due to a point charge. Charge has its effects on its surroundings and that’s why it affects the potential in it’s surrounding.

Now if another charge is placed near a source charge there will be some effect in a potential. Let’s derive the expression for potential due to a point charge.

Here we have a source charge and another charge will be brought from infinity to a point A. We will derive an expression of potential at that point A due to source charge Q.

Q is a charge and we have to find the potential at point A at distance r.

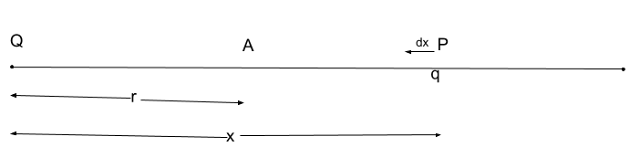Electric potential due to a point charge diagram

Let there be a point P at distance x, here charge q is been placed. So force on the test charge ‘q‘:

Electric potential due to a point charge derivation

To move it to a small distance ‘dx’ the work done is:

To work done :

So,

Now after finding the work done, potential at a point is work done on a unit charge.

Therefore, potential at a point will be :

Hence Potential at a point due to a point charge is:

Now we know that electric potential due to a point charge and after deriving the expression of electric potential we are now ready to find the electric potential at the centre of a ring.

Electric potential at the centre of the ring:

Electric Potential at the centre of the charged ring

Imagine a circular ring with radius ‘r’ and ϴ is the angle between the reference line ‘A’ to point on the ring. dӨ is the small angle from a point on the surface. The length of line A = radius of ring (∵ line A is the reference line from the centre to surface)

Potential on the centre due to dӨ is:

Electric Potential at the centre of the charged ring derivation

To find the total potential to the ring at the centre we need to integrate the above equation.

P.s:- ‘k’ in the above equation represents constant and ‘r’ represents the radius.

This is the potential at the centre of the charged ring. We will notice that the equation of electric potential at the centre of the ring is the same as the electric potential due to a point charge.

To understand the reason behind is, you can imagine that circular ring is nothing but will behave like a charge if we compare it to heavy bodies such as moon or earth. So that’s why electric potential equation for point charge and at the centre of the ring is the same,

Ring behaves as point charge due to which equation of potential difference is same for both of them

Conclusion:

To understand the concept clearly, you will need to understand that electric potential is the work done on bringing a unit charge from infinity to a point and the electric potential difference is the difference between the potential of two points.

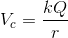Electric potential at the centre of the ring is the same as that of electric potential due to a point charge.

F.AQ:

Q.1 Why electric field inside a ring is zero but the potential is not ?

Electric field is a vector quantity so it has magnitude as well as direction and due to this, electric field due to half ring is cancelled out by another half due to the opposite direction but electric potential is a scalar quantity due to which it doesn’t get cancelled out.

Q.2 How is electric potential and potential difference not the same ?

Electric potential is work done on a unit charge when bringing from infinity to a point. Whereas potential difference is the difference in electrical potential between two points.

Q.3 What is potential ?

Potential is the characteristic of a location.

Q.4 What does ‘r’ refer to in the equation of electric potential due to point charge ?

‘r’ is the distance between point and charge.

Electric Potential at the Centre of a Ring – Derivation and Explanation